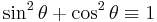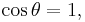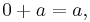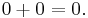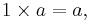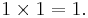Identity (mathematics)

In mathematics, the term identity has several different important meanings:

An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of the involved variables. Definitions are often indicated by the 'triple bar' symbol ≡, such as A² ≡ x·x. The symbol ≡ can also be used with other meanings, but these can usually be interpreted in some way as a definition, or something which is otherwise tautologically true (for example, a congruence relation).

In algebra, an identity or identity element of a set S with a binary operation · is an element e that, when combined with any element x of S, produces that same x. That is, e·x = x·e = x for all x in S. An example of this is the identity matrix.

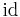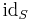The identity function from a set S to itself, often denoted $\mathrm{id}$ or $\mathrm{id}_S$ , is the function which maps every element to itself. In other words, 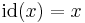$\mathrm{id}(x) = x$ for all x in S. This function serves as the identity element in the set of all functions from S to itself with respect to function composition.

1 Examples
2 Comparison
3 External links

Examples

Identity relation

A common example of the first meaning is the trigonometric identity

$\sin ^2 \theta %2B \cos ^2 \theta \equiv 1\,$

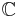which is true for all complex values of $\theta$ (since the complex numbers $\Bbb{C}$ are the domain of sin and cos), as opposed to

$\cos \theta = 1,\,$

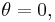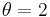which is true only for some values of $\theta$ , not all. For example, the latter equation is true when $\theta = 0,\,$ false when $\theta = 2\,$ .

Identity element

The concepts of "additive identity" and "multiplicative identity" are central to the Peano axioms. The number 0 is the "additive identity" for integers, real numbers, and complex numbers. For the real numbers, for all 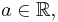$a\in\Bbb{R},$

$0 %2B a = a,\,$

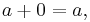$a %2B 0 = a,\,$ and

$0 %2B 0 = 0.\,$

Similarly, The number 1 is the "multiplicative identity" for integers, real numbers, and complex numbers. For the real numbers, for all 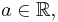$a\in\Bbb{R},$

$1 \times a = a,\,$

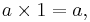$a \times 1 = a,\,$ and

$1 \times 1 = 1.\,$

Identity function

A common example of an identity function is the identity permutation, which sends each element of the set 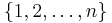$\{ 1, 2, \ldots, n \}$ to itself or 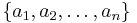$\{a_1,a_2, \ldots, a_n \}$ to itself in natural order.

Comparison

These meanings are not mutually exclusive; for instance, the identity permutation is the identity element in the group of permutations of 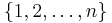$\{ 1, 2, \ldots, n \}$ under composition.

External links

A Collection of Algebraic Identities
EquationSolver – A webpage that can test a suggested identity and return a true/false "verdict".